![]()
by Glenn R. Smith
![]()
by Glenn R. Smith
|
A thirteenth century mathematician named Leonardo Fibonacci created a recreational game that goes as follows: "How many pairs of rabbits can be produced from a single pair in one year if it as assumed that every month each pair begets a new pair which from the second month becomes productive?" Starting with one pair the following sequence is generated: |
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| # of pairs | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 |
|
The second row represents the first twelve terms of what is now called the Fibonacci series. The series can be continued indefinitely based on the simple rule: each terms is found by adding the two terms immediately preceding. (except the very first two terms.) Four hundred years after Fibonacci an important relationship was formulated for this series.
Since then, especially in our present century, The properties of the Fibonnaci numbers have been studied extensively. From all of the literature resulting therfrom, an important ratio is recognised. The ratio is so intriguing that it has been designated The Golden Number and is represented as the greek letter PHI. The ratio is as follows: Take the square root of five and add one. Divide the result by two and you have the Golden Number. Other interesting things about PHI are that its reciprocal is the same as the fractional part. PHI squared changes its integer but retains the same fractional part.
Lets continue by examining the first 48 terms of the Fibonacci series.
By applying the rules of the game the single pair of hypothetical rabbits would have generated 4,807,526,976 pairs by the end of the fourth year! If you divide any number of this series by the number immediately preceding it you will get the golden mean or 1.618. Only that the higher up in the series the closer to the average mean you will get. Besides being an interesting number game, the Fibonacci series exemplifies biological growth patterns such as phyllotaxis. The arrangement of the whorls on a pinecone or pineapple, of petals on a sunflower, and of branches from some stems follow the sequence of Fibonacci numbers. Also the logarithmic spirals found on a cross section of a nautilus shell, the basic proportions of the human body and periodic cycles of some planets relate to this series as well. The rest of this article will focus on some of these relationships.
The spiral, as found in a Nautilus shell, is illustrated above. The radius point for each consecutive 90 degree arc is moved at a value equaling the side divided by PHI. In this case r represents the side and s represents r/PHI.
The PentacleOf all symmetric geometric shapes, none represent so concisely the principles of PHI than the pentacle or five pointed star within a circle. This is probably so because the ratio of PHI is first derived from the square root of five. Using a compass, draw a circle with five points spaced at exactly 72 degree apart with the first point at the top. Connect the points at 144 degree intervals with straight lines. Notice that both numbers 5 and 144 occur in the first twelve terms of the Fibonacci series.Draw a straight line from the center of the circle intersecting the two bottom "legs" of the star. That line is equal to the radius of the circle. Measure the radius in centimeters. Measure the portion of the radius that lies outside the star. Divide the radius by the portion outside the star and the number is PHI. Measure the length of the straight line between any two points of the star. (You will notice that the line will be intersected twice by the lines going to the point adjacent to the points you are measuring.) Now measure the section of the line going from one point to the farther intersecting place from that point. The length of the whole line divided by the section equals PHI. 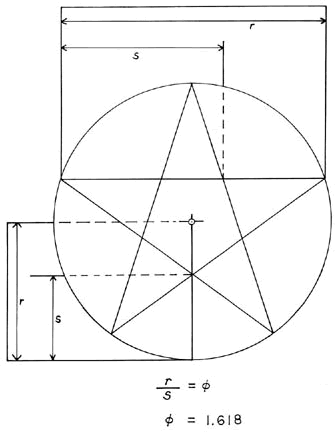
The human body looks something like a five pointed star. Stretch out your arms straight to each side of you and have someone measure the distance from your fingertips left to right. Take this measure and divide it by the distance from on fingertip to the opposite shoulder and the result is close to PHI. Measure your height from heel to top of head. Divide this measure by the distance from heel to navel and the result is close to PHI. I say close to PHI because everybody has a unique proportion that slightly differs from person to person. Only an average of PHI is to be sought by these personal measurements. Also as mentioned earlier, the terms farther along the Fibonacci series yield results closer to PHI than those of the earlier terms of the series. In this sense we might understand that human proportions rarely go beyond the ratios represented by the first ten terms of the series.
Earth and VenusThe Earth completes one orbit around the the Sun in 365 days. The orbit of the circle contains 360 degrees. The only number that will divide both 360 and 365 without leaving a remainder is 5. So the ratio of the Earth's orbit to the Earth's rotation is:
Taken at an average we can say that for every 72 degrees the Earth travels in its orbit, it will make 73 rotations on its axis relative to the sun. Thus we can say that this ratio marks out a natural pentacle in space. The synodic period of Venus, the time it takes for two consecutive inferior conjunctions with the Sun, is 584 days. Five such synodic periods of Venus is 2920 days. This is equal to eight Earth years of 365 days. Here we see the ratio 8:5 whereas 8 Earth years equal 5 synodic Venus cycles. As you look at the terms in the Fibonacci series you notice the two numbers 5 and 8. Take one synodic Venus cycle of 584 days and divide it by 8. The result is 73, the number of days it takes for the Earth to complete 1/5 of its orbit around the Sun. Incidently, it should be noted that the Mayan Calendar uses the Earth-Venus cycles as a basis for their reckoning system. PHI and the Fibonacci series keeps popping up when examining the Mayan Calendar.
Sidereal Earth to Venus: 100 steps of 73 days December 4th 1950 to September 17th 1970. The above figure shows the relationship of the Earth and Venus. Viewed as above the solar system looking down on the planets with the Sun placed in the center. To the right is sidereal Aries; to the top is sidereal Cancer; to the left is sidereal Libra and to the bottom is sidereal Capricorn. Lines are drawn connecting the respective positions of Earth and Venus after every 73 Earth days in their orbits. This is repeated a hundred steps. You can see the pentagonal pattern developed by their orbits.
Venus from Earth: 975 steps of 3 days, January 1st 1985 to January 1st 1993. A critic might charge that any period of orbit divided into steps that favor pentagonal patterns can be arbitrarily chosen to prove anything. To counter this charge, we will choose a number that would not normally be a pentagonal divisor of the orbiting period of either planet. In the illustration above we plot points rather than lines at the point where two consecutive lines would intersect. Points are plotted every three days for 975 steps. Even with a non-pentagonal divisor of the orbital period we can still see a five petaled flower pattern.
Jupiter and SaturnFor every complete orbit of Jupiter, Saturn will travel about 144 degree along its orbit. So after 60 years, Jupiter will have made 5 complete orbits while Saturn will have marked out five points, each 144 degrees apart. While doing so Saturn will have made two complete orbits.
Here we see again the numbers 5 and 144 of the Fibonacci series. But whereas the Earth-Venus cycles contain mostly Fibonacci values, the Jupiter-Saturn relationship contains more. It has the patterns of the Fibonacci and the sexagesimal. As the pentacle was shown to have a relationship with PHI, the sexagesimal (hexagram) has a relationship to PI, that other magical number. And, as will be shown, both PHI and PI have a relationship to each other. PI is the number that represents the ratio of the diameter of a circle to its circumference. PI to four decimal places is 3.1416. PI divided by 2 represents that ratio in regard to the radius of a circle. And, as we know, the radius of a circle measured in a straight line divides a circle into six parts. Hence the hexagram. As explained in a previous article, (The Six Thousand Year Barrier), the 60 year cycle of Jupiter and Saturn gives rise to the usage of the sexagesimal system and its derivatives.
PITake the reciprocal of PHI (.618) and cube it. Multiply that by 6 and divide the result by ten. Add to this 3 and you have PI to four decimal places.
In summary I will not draw any definite conclusions but instead offer suggestions. While this article may not prove to have any valuable application, it serves as an example of the insight we may get when we study the relationship between things rather than just the things themselves. Patterns of interaction and processes can be just as interesting as the things that create the patterns. Such patterns appeal to a certain symbolic part of our consciousness which creates the reality we live in. I believe that it is this usage of symbolic patterns that enabled the mystics, magicians and alchemist to practice their philosophy. And it may be argued that mathematics evolved from symbolic logic and pattern recognition. Who knows? By reading this perhaps some magick spell may work on your consciousness and bring it to another level of awareness. |